Características

Dominio y Recorrido

1.

El dominio de una función son los valores que toma la x
Se expresa en intervalos.
Se mira el eje de abscisas o eje X.
Se expresa como Dom f(x)

El recorrido o imagen son los valores que toma la variable y.
Se expresa en intervalos.
Nos fijamos en el eje de ordenadas o eje y.
Se expresa como Rec f(x) o Im f(x)

-Hay que tener tener especial cuidado con las discontinuidades.

-Tanto en el dominio como en el recorrido se utiliza la "U" para unir los distintos tramos de intervalo.

-Atención a los puntos abiertos (se indican con paréntesis) y los cerrados (con corchetes [ ] )

Ejemplos:

Dom f(x) = (-∞, -1)U(-1, +∞ )

Rec f(x) = (-∞, +∞)

Dom f(x) = (0,9)

Rec f(x) = (0, 140)

Dom f(x) = (-4,2)U(2,6 )

Rec f(x) = (-4,4)

2. puntos de corte con los ejes

Puntos de corte con el eje X

Nos debemos fijar dónde la curva corta el eje de abscisas o eje X
Son PUNTOS, por lo que deben tener dos coordenadas, x, e y.
Son de la forma: (nº, 0)

Puntos de corte con el eje Y

Nos debemos fijar dónde la curva corta el eje de ordenadas o eje Y
Al igual que los puntos de corte con el eje X, Son PUNTOS, por lo que deben tener dos coordenadas, x, e y.
Son de la forma: (0, nº)

NO se utiliza la "U", ya que NO SON INTERVALOS.

Ejemplos:

Puntos de corte EJE X: (-3,5, 0), (-1,4; 0) y (2,0)

Puntos de corte EJE Y: (0,3)

Puntos de corte EJE X: (-2,7; 0), (-1,5; 0) y (0,0)

Puntos de corte EJE Y: (0,0)

3. SIGNO DE LA FUNCIÓN

La función es POSITIVA cuando la curva está por encima del eje X
La función es NEGATIVA cuando la curva está por debajo del eje X.
La función es NEUTRA cuando la curva está encima del eje X.

El signo de la función se expresa en intervalos.
Nos fijaremos siempre en el eje X.

4. SIMETRÍA

La función puede:

SER SIMÉTRICA PAR: Presenta una simetría respecto al eje y.

SER SIMÉTRICA IMPAR: Presenta una simetría respecto al origen de coordenadas

NO PRESENTAR SIMETRÍA

5. CRECIMIENTO Y DECRECIMIENTO

Una función es creciente cuando la pendiente es positiva.

Una función es decreciente cuando la pendiente es negativa.

Se expresan mediante intervalos, por lo que utilizaremos la "U" para unir las diferentes partes, si es que las hubiese.
Nos fijamos en el EJE X.

6. MÁXIMOS Y MÍNIMOS.

Máximos:

Nos debemos fijar dónde la función cambia de decreciente a creciente, es decir, tienen forma de montaña o de pico.
Son PUNTOS, por lo que deben tener dos coordenadas, x, e y.

Mínimos:

Nos debemos fijar dónde la función cambia de creciente a decreciente, es decir, tienen forma de valle.
Son PUNTOS, por lo que deben tener dos coordenadas, x, e y.

Creciente en los intervalos:(-4,-2)U(-1,6)

Decreciente en el intervalo (-2, -1)

Máximo: (-2,1)

Mínimo: (-1,-1)

Creciente en los intervalos:(-3,-1)U(0;1,5)

Decreciente en los intervalos: (-3,-2)U(-1,0)

Máximo: (-1,1)

Mínimo: (0,-4)

7. Continuidad

Las funciones pueden presentar 3 tipos de discontinuidades:

1. Discontinuidad evitable: es la que se puede redefinir en dicho punto para convertirla en una función continua. Es decir, falta un punto, Si existiera la imagen de ese punto en la función, sería continua.

2. Discontinuidad de salto finito: la función presenta un salto en el que se puede apreciar la distancia que hay entre las distintas ramas de la función.

3. Discontinuidad de salto infinito: La función presenta un salto, pero esta vez no se puede distinguir la distancia que hay entre las distintas ramas, ya que la distancia entre ellas es infinita.

Las discontinuidades se expresan así: "En x= ___, hay una discontinuidad de tipo ________________"

Ejemplo:

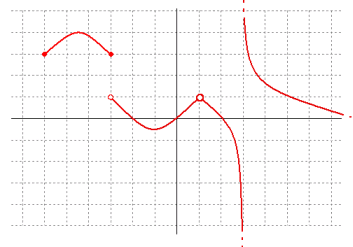
La función no es continua y presenta las siguientes discontinuidades:

En x=-3 encontramos una discontinuidad de tipo salto finito.
En x=1 encontramos una discontinuidad evitable.
En x=4 hay una discontinuidad de tipo salto infinito.

8. Periodicidad

Las funciones periódicas son funciones que se comportan en una manera cíclica (repetitiva) sobre un intervalo especificado (llamado un periodo). La gráfica se repite a si misma una y otra vez así como es trazada de izquierda a derecha.

En el caso de que la función sea periódica, se debe especificar el período (T).

La función es periódica con T=4